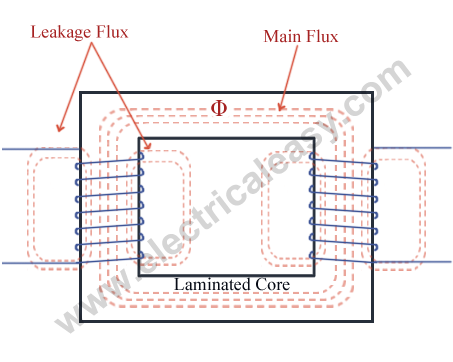
Magnetic leakage
In a transformer it is observed that, all the flux linked with primary winding does not get linked with secondary winding. A small part of the flux completes its path through air rather than through the core (as shown in the fig at right), and this small part of flux is called as leakage flux or magnetic leakage in transformers. This leakage flux does not link with both the windings, and hence it does not contribute to transfer of energy from primary winding to secondary winding. But, it produces self induced emf in each winding. Hence, leakage flux produces an effect equivalent to an inductive coil in series with each winding. And due to this there will be leakage reactance.
(To minimize this leakage reactance, primary and secondary windings are not placed on separate legs, refer the diagram of core type and shell type transformer from construction of transformer.)
(To minimize this leakage reactance, primary and secondary windings are not placed on separate legs, refer the diagram of core type and shell type transformer from construction of transformer.)
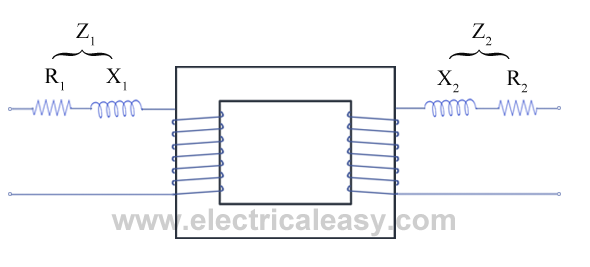
Practical Transformer with resistance and leakage reactance
In the following figure, leakage reactance and resitance of the primary winding as well as secondary winding are taken out, representing a practical transformer.
Where, R1 and R2 = resistance of primary and secondary winding respectively
X1 and X2 = leakage reactance of primary and secondary winding resp.
Z1 and Z2 = Primary impedance and secondary impedance resp.
Z1 = R1 + jX1 ...and Z2 = R2 + jX 2 .
The impedance in each winding lead to some voltage drop in each winding. Considering this voltage drop the voltage equation of transformer can be given as -
V1 =E1 + I 1(R1 + jX1 ) --------primary side
V2 = E2 - I2(R2 + jX2 ) --------secondary side
where, V1 = supply voltage of primary winding
V2 = terminal voltage of secondary winding
E1 and E2 = induced emf in primary and secondary winding respectively. (EMF equation of a transformer.)
Z1 = R1 + jX1 ...and Z2 = R2 + jX 2 .
The impedance in each winding lead to some voltage drop in each winding. Considering this voltage drop the voltage equation of transformer can be given as -
V1 =
V2 = E2 - I2(R2 + jX2 ) --------secondary side
where, V1 = supply voltage of primary winding
V2 = terminal voltage of secondary winding
E1 and E2 = induced emf in primary and secondary winding respectively. (EMF equation of a transformer.)