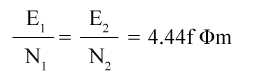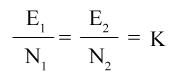In a transformer, source of alternating current is applied to the primary winding. Due to this, the current in the primary winding (called as magnetizing current) produces alternating flux in the core of transformer. This alternating flux gets linked with the secondary winding, and because of the phenomenon of mutual induction an emf gets induced in the secondary winding. Magnitude of this induced emf can be found by using the following EMF equation of the transformer.
N1 = Number of turns in primary winding
N2 = Number of turns in secondary winding
Φm = Maximum flux in the core (in Wb) = (Bm x A)
f = frequency of the AC supply (in Hz)
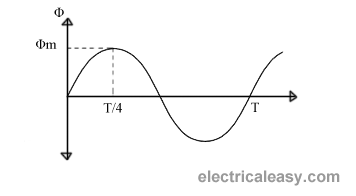
As, shown in the fig., the flux rises sinusoidally to its maximum value Φm from 0. It reaches to the maximum value in one quarter of the cycle i.e in T/4 sec (where, T is time period of the sin wave of the supply = 1/f).
Therefore,
average rate of change of flux = Φm /(T/4) = Φm /(1/4f)
Therefore,
average rate of change of flux = 4f Φm ....... (Wb/s).
Now,
Induced emf per turn = rate of change of flux per turn
Therefore, average emf per turn = 4f Φm ..........(Volts).
Now, we know, Form factor = RMS value / average value
Therefore, RMS value of emf per turn = Form factor X average emf per turn.
As, the flux Φ varies sinusoidally, form factor of a sine wave is 1.11
Therefore, RMS value of emf per turn = 1.11 x 4f Φm = 4.44f Φm.
RMS value of induced emf in whole primary winding (E1) = RMS value of emf per turn X Number of turns in primary winding
E1 = 4.44f N1 Φm ............................. eq 1
Similarly, RMS induced emf in secondary winding (E2) can be given as
E2 = 4.44f N2 Φm. ............................ eq 2
from the above equations 1 and 2,
This is called the emf equation of transformer, which shows, emf / number of turns is same for both primary and secondary winding.
For an ideal transformer on no load, E1 = V1 and E2 = V2 .
where, V1 = supply voltage of primary winding
V2 = terminal voltage of secondary winding
Where, K = constant
This constant K is known as voltage transformation ratio.
EMF equation of the Transformer
Let,N1 = Number of turns in primary winding
N2 = Number of turns in secondary winding
Φm = Maximum flux in the core (in Wb) = (Bm x A)
f = frequency of the AC supply (in Hz)
As, shown in the fig., the flux rises sinusoidally to its maximum value Φm from 0. It reaches to the maximum value in one quarter of the cycle i.e in T/4 sec (where, T is time period of the sin wave of the supply = 1/f).
Therefore,
average rate of change of flux = Φm /(T/4) = Φm /(1/4f)
Therefore,
average rate of change of flux = 4f Φm ....... (Wb/s).
Now,
Induced emf per turn = rate of change of flux per turn
Therefore, average emf per turn = 4f Φm ..........(Volts).
Now, we know, Form factor = RMS value / average value
Therefore, RMS value of emf per turn = Form factor X average emf per turn.
As, the flux Φ varies sinusoidally, form factor of a sine wave is 1.11
Therefore, RMS value of emf per turn = 1.11 x 4f Φm = 4.44f Φm.
RMS value of induced emf in whole primary winding (E1) = RMS value of emf per turn X Number of turns in primary winding
E1 = 4.44f N1 Φm ............................. eq 1
Similarly, RMS induced emf in secondary winding (E2) can be given as
E2 = 4.44f N2 Φm. ............................ eq 2
from the above equations 1 and 2,
For an ideal transformer on no load, E1 = V1 and E2 = V2 .
where, V1 = supply voltage of primary winding
V2 = terminal voltage of secondary winding
Voltage Transformation Ratio (K)
As derived above,
This constant K is known as voltage transformation ratio.
- If N2 > N1, i.e. K > 1, then the transformer is called step-up transformer.
- If N2 < N1, i.e. K < 1, then the transformer is called step-down transformer.
