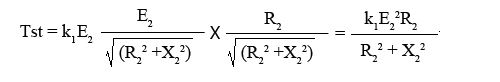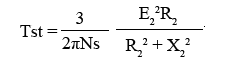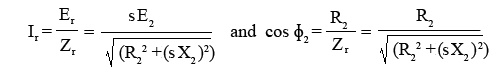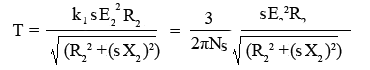Torque of a three phase induction motor is proportional to flux per stator pole, rotor current and the power factor of the rotor.
T ∝ ɸ I2 cosɸ2 OR T = k ɸ I2 cosɸ2 .
where, ɸ = flux per stator pole,
I2 = rotor current at standstill,
ɸ2 = angle between rotor emf and rotor current,
k = a constant.
Now, let E2 = rotor emf at standstill
we know, rotor emf is directly proportional to flux per stator pole, i.e. E2 ∝ ɸ.
therefore, T ∝ E2 I2 cosɸ2 OR T =k1 E2 I2 cosɸ2.
T ∝ ɸ I2 cosɸ2 OR T = k ɸ I2 cosɸ2 .
where, ɸ = flux per stator pole,
I2 = rotor current at standstill,
ɸ2 = angle between rotor emf and rotor current,
k = a constant.
Now, let E2 = rotor emf at standstill
we know, rotor emf is directly proportional to flux per stator pole, i.e. E2 ∝ ɸ.
therefore, T ∝ E2 I2 cosɸ2 OR T =k1 E2 I2 cosɸ2.
Starting torque
The torque developed at the instant of starting of a motor is called as starting torque. Starting torque may be greater than running torque in some cases, or it may be lesser.
We know, T =k1 E2 I2 cosɸ2.
let, R2 = rotor resistance per phase
X2 = standstill rotor reactance
then,
Therefore, starting torque can be given as,
The constant k1 = 3 / 2πNs
Condition for maximum starting torque
If supply voltage V is kept constant, then flux ɸ and E2 both remains constant. Hence,
Hence, it can be proved that maximum starting torque is obtained when rotor resistance is equal to standstill rotor reactance. i.e. R22 + X22 =2R22 .
Torque under running condition
T ∝ ɸ Ir cosɸ2 .
where, Er = rotor emf per phase under running condition = sE2. (s=slip)
Ir = rotor current per phase under running condition
reactance per phase under running condition will be = sX2
therefore,
as, ɸ ∝ E2.
Maximum torque under running condition
Torque under running condition is maximum at the value of slip (s) which makes rotor reactance per phase equal to rotor resistance per phase.